Octahedron
(f = 8, e = 12, v = 6) 

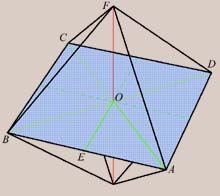
Like the cube, the octahedron's ex- and inradius are very easy to determine. As usual, we let the side of the octahedron have length 1. Thus AE = 1/2. Now, it is clear that ABCD is a square (from symmetry). Then O is the center of this square, and is the foot of the perpendicular dropped from vertex F. Thus OE = EA, and OA = OB = OF. So OA = Sqrt[2]/2 = 1/Sqrt[2], which is the exradius R_o. To find the inradius, not shown here, we construct the perpendicular from point O to the center of equilateral triangle ABF at G. AGO being right, GO² + AG² = OA². Since AG² = EG² + EA² = 4/3 EA², r_o² = GO² = OA² - 4/3 EA² = 1/2 - (4/3)(1/4) = 1/6, and r_o = 1/Sqrt[6].