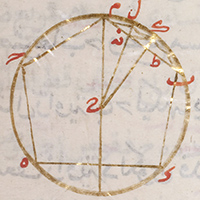
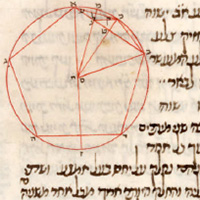
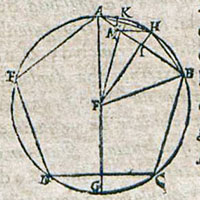
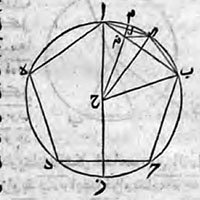

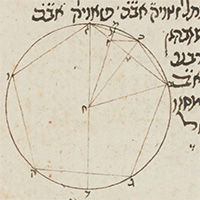
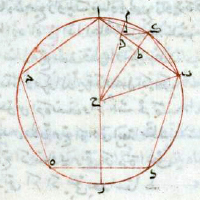

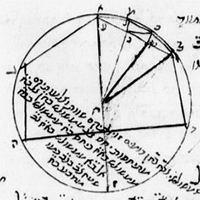
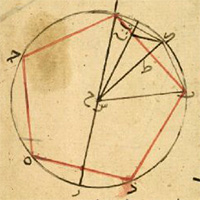

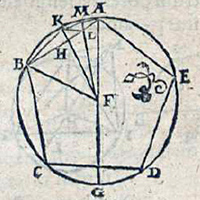
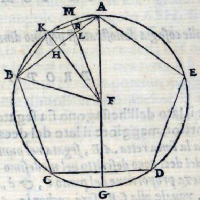

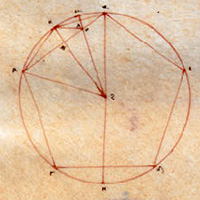
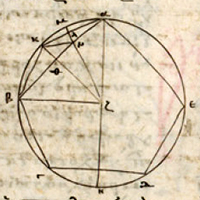
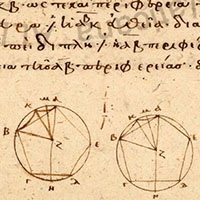
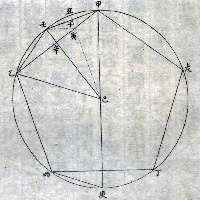
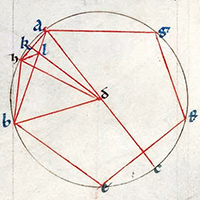

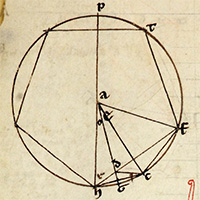
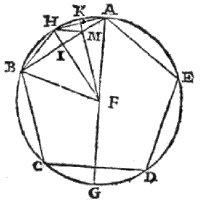
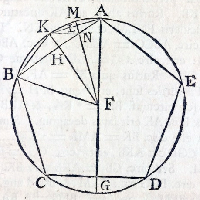
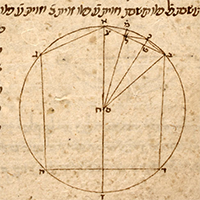
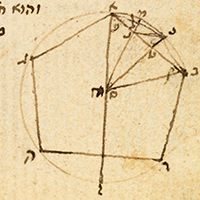

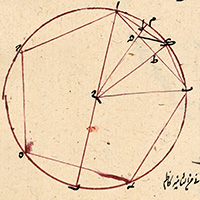
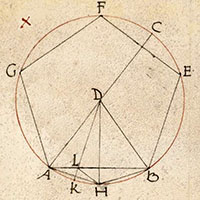
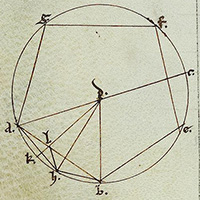


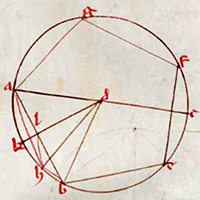
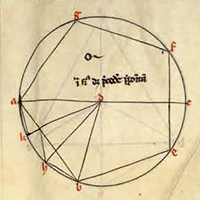
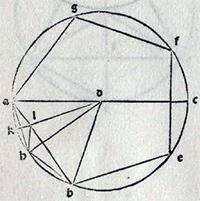
de la Figure XIII.10
dans les manuscrits
de la BnF
des figures XIII.7 à 11
dans les manuscrits
de la Biblioteca
Vaticana


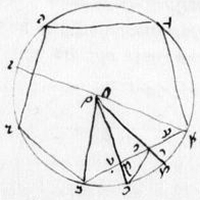

|
 |
 |  |  |
|||
 |
 |
 |
 |

|
 |
 |
 |
 |
 |
 |
 |
 | |||
 |
 |
 |
 |

|
|||
 |
 |
 |
 |
 |
|||
 |

|
 | 
|
 | 
|
||
| Description de la Figure XIII.10 dans les manuscrits de la BnF |
Description des figures XIII.7 à 11 dans les manuscrits de la Biblioteca Vaticana |
 |
 |
 |
|||



 |
  |



