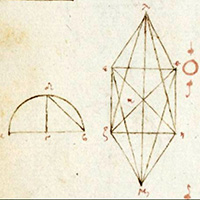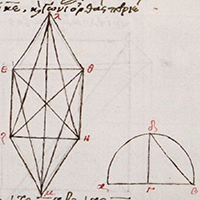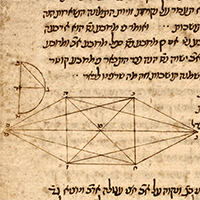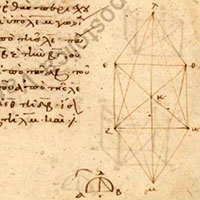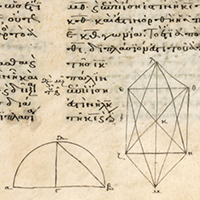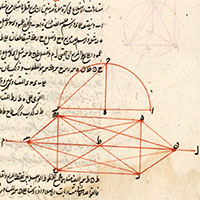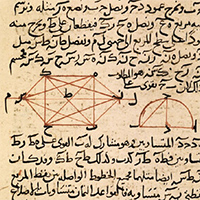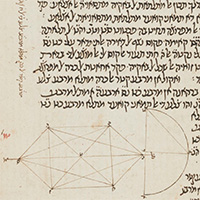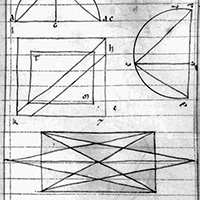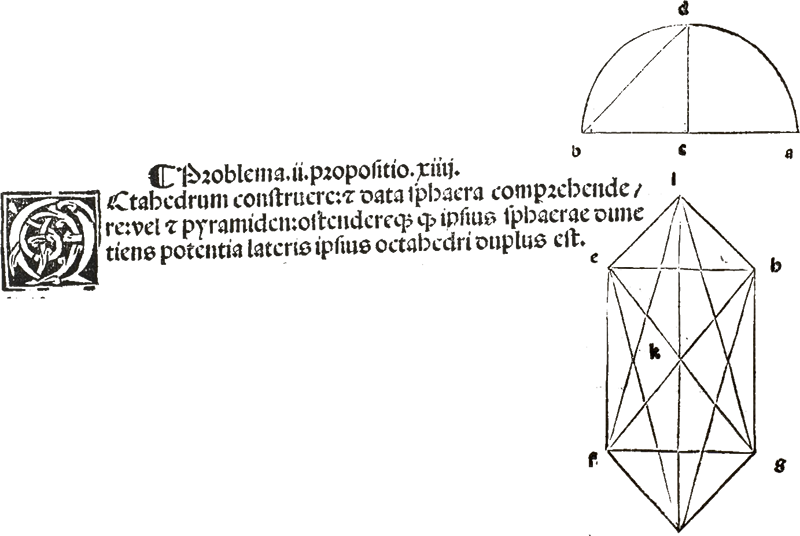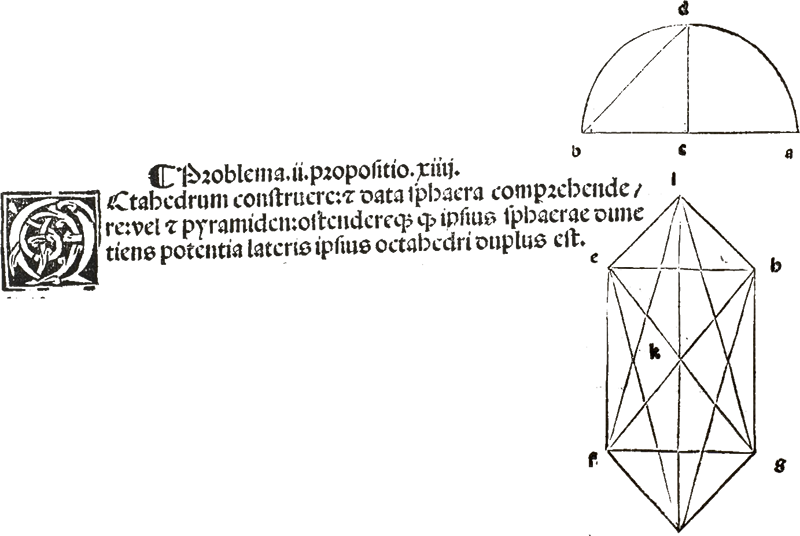



Proposition
14. To construct an octahedron and comprehend it in a sphere,
and to prove that the square on the diameter of the sphere is double the square on the side of the octahedron.
Proposición
14. Construir un octaedro inscrito en una esfera,
y demostrar que el cuadrado del diámetro de la esfera es el doble del cuadrado del lado del octaedro.
Proposició
14. Construir un octaedre i inscrit en una esfera,
i demostrar que el quadrat del diàmetre de l´esfera és el doble del quadrat del costat de l´octaedre.
Construir um octaedro e contê-lo por uma esfera, como nas coisas
anteriores, e provar que o diâmetro da esfera é, em potência, o dobro do
lado do octaedro.

α ? Σ ©
..