BOOK I.
THEORY OF ANGLES, TRIANGLES, PARALLEL LINES, AND PARALLELOGRAMS.
DEFINITIONS.
The Point. i. A point is that which has position but not dimensions.
A geometrical magnitude which has three dimensions, that is, length, breadth, and thickness, is a solid; that which has two dimensions, such as length and breadth, is a surface; and that which has but one dimension is a line. But a point is neither a solid, nor a surface, nor a line; hence it has no dimensions : that is, it has neither length, breadth, nor thickness.




BOOK I. PROP. II.—Problem.
From a given point to draw a right line equal to a given finite right line.





BOOK I. PROP. XXII.—Problem.
To construct a triangle whose three sides shall be respectively equal to three
given lines, the sum of every two of which is greater than the third.






BOOK I. PROP. XLVII.—Theorem.
In a right-angled triangle the square on the hypotenuse is equal to the sum of the squares on the other two sides





BOOK II. PROP. V.—Theorem.
If a line be divided into two equal parts, and also into two unequal parts,
the rectangle contained by the unequal parts, together with the square on the part between the points of section,
is equal to the square on half the line.





BOOK II. PROP. VII.—Theorem.
If a right line be divided into any two parts, the sum of the squares on the whole line and either segment
is equal to twice the rectangle contained by the whole line and that segment, together with the square on the other segment.





BOOK II. PROP. VIII.–Theorem.
If a line be divided into two parts, the square on the sum of the whole line and either segment
is equal to four times the rectangle contained by the whole line and that segment, together with the square on the other segment.





BOOK II. PROP. XI.—Problem.
To divide a given finite line into two segments,
so that the rectangle contained by the whole line and one segment may be equal to the square on the other segment.





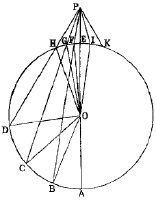
BOOK III. PROP. VIII.—Theorem.
If from any point outside a circle, lines be drawn to the concave circumference, then :
1. The maximum is that which passes through the centre.
2. Of the others, that which is nearer to the one through the centre is greater than the one more remote.
3. The minimum is that whose production passes through the centre.
4. Of the others, that which is nearer to the minimum is less than one more remote.
5. From the given point there can be drawn two equal lines to the concave or the convex circumference,
both of which make equal angles with the line passing through the centre.
6. More than two equal lines cannot be drawn from the given point to either circumference.






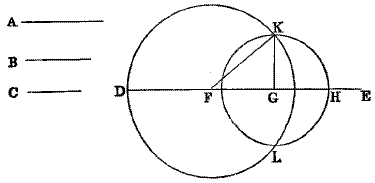
BOOK III. PROP. XXXV.—Theorem.
If two chords of a circle intersect in a point within the circle, the rectangles contained by the segments are equal.






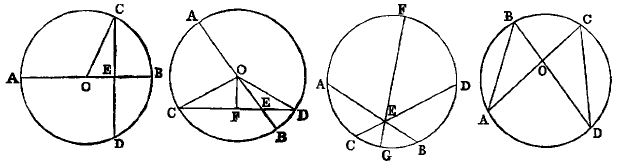
BOOK III. PROP. XXXVI.—Theorem.
If from any point without a circle two lines be drawn to it, one of which is a tangent, and the other a secant,
the rectangle contained by the segments of the secant is equal to the square of the tangent.





BOOK III. PROP. XXXVII.—Theorem.
If the rectangle contained by the segments of a secant, drawn from any point without a circle,
be equal to the square of a line drawn from the same point to meet the circle,
the line which meets the circle is a tangent.





BOOK IV. PROP. I.—Problem.
In a given circle to place a chord equal to a given line not greater than the diameter.





BOOK IV. PROP. X.—Problem.
To construct an isosceles triangle having each base angle double the vertical angle.





BOOK VI. PROP. I.—Theorem.
Triangles and parallelograms which have the same altitude are to one another as their bases.






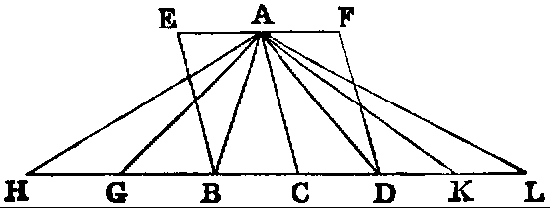
BOOK VI. PROP. XX.—Theorem.
Similar polygons may be divided into the same number of similar triangles;
the corresponding triangles have the same ratio to one another which the polygons have;
the polygons are to each other in the duplicate ratio of their homologous sides.





BOOK VI. PROP. XXVII—Problem.
To inscribe in a given triangle the maximum parallelogram having a common angle with the triangle.






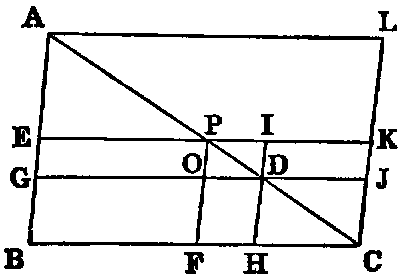
BOOK VI. PROP. XXVIII.—Problem.
To inscribe in a given triangle a parallelogram equal to a given rectilineal figure not greater than the maximum inscribed parallelogram,
and having an angle common with the triangle.






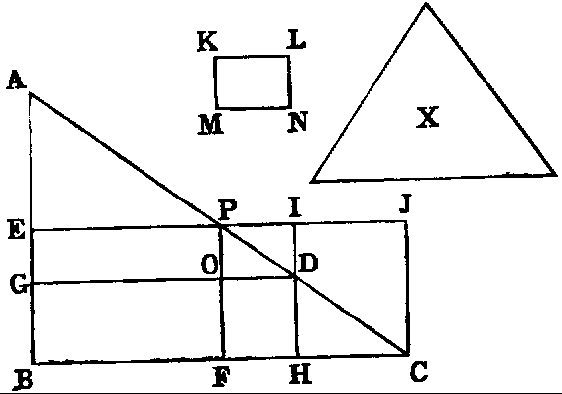
BOOK VI. PROP. XXIX.—Problem.
To escribe to a given triangle a parallelogram equal to a given rectilineal figure,
and having an angle common with an external angle of the triangle.






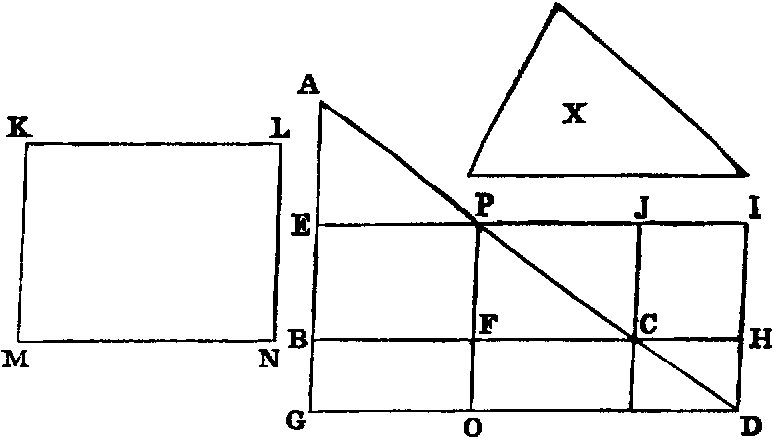
BOOK VI. PROP. XXXIII.–Theorem.
In equal circles, angles at the centres or at the circumferences have the same ratio to one another
as the arcs on which they stand, and so also have the sectors.












©       α       ?       Σ